Back to research highlights

1. Prediction of fluid velocity distribution from pore structure in porous media (MIT, UT-Austin)

Research thrusts: Fast & reliable solution of multiphysics/multiscale problems
Research sub-thrusts: Fast solvers; Accurate & robust discretizations; Coarse graining

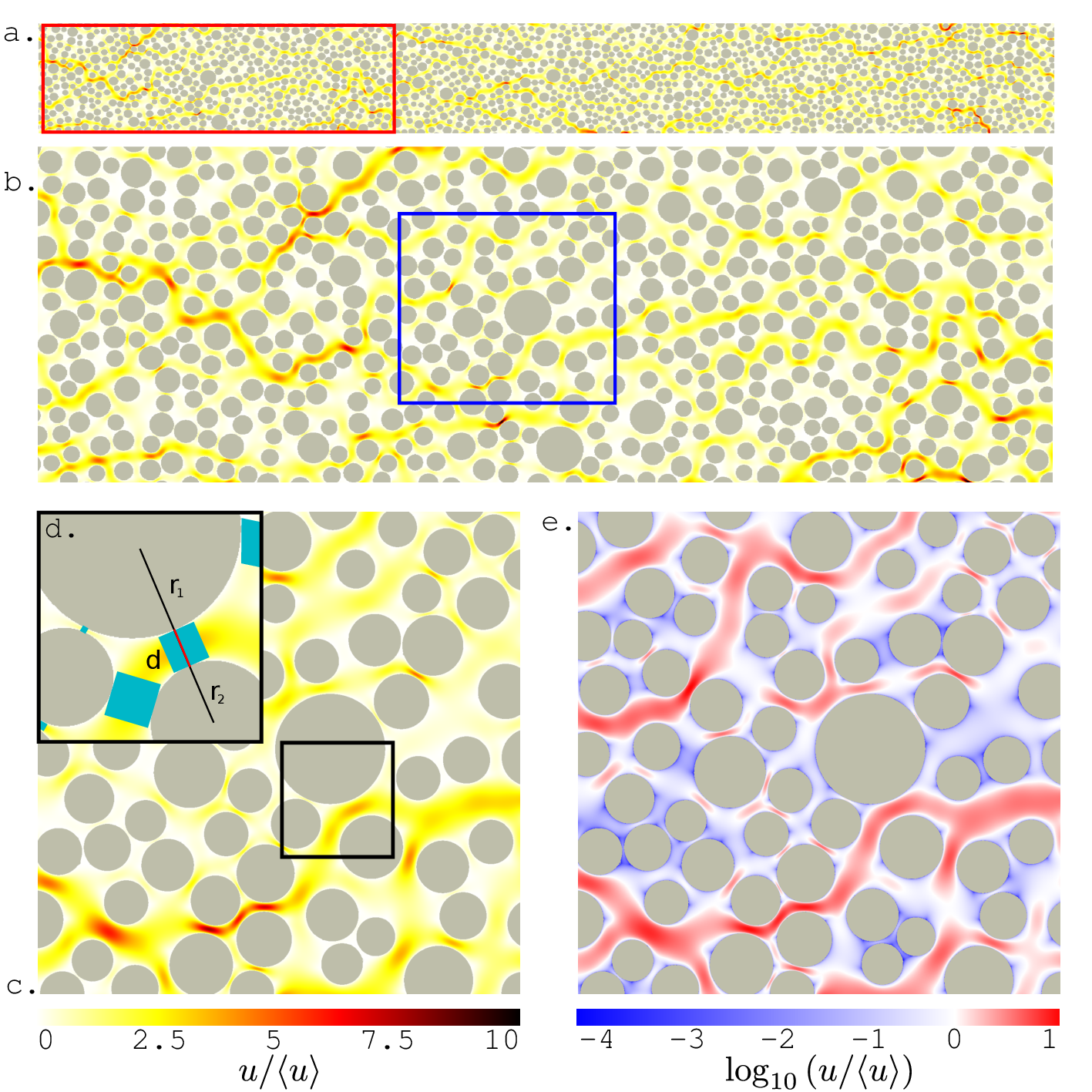
Porous media flows have a rich structure, and this spatial and temporal complexity plays a critical role in natural and engineered processes such as groundwater contamination and remediation, water infiltration in soil, geologic carbon sequestration, enhanced hydrocarbon recovery, water filtration systems, and polymer electrolyte fuel cells. Understanding and quantifying velocity heterogeneity in porous media is important because it controls particle spreading and fluid mixing, which often mediates chemical reactions and biological activity. The groups of co-PI Juanes at MIT and co-PI Biros at UT Austin have been collaborating to address a long-standing challenge in porous media flows: predicting the relationship between pore structure and velocity distribution from Stokesian flow through the pore space [42]. We derive an analytical relationship between the pore throat size distribution fλ ~ λ-β and the distribution of fluid velocity fu ~ u-β∕2, based on a conceptual model of porelets—Hagen–Poiseuille flows established within each pore throat. Our model allows us to make predictions for the statistics of spreading of fluid particles along their own trajectories, which are confirmed by high fidelity simulations of Stokes flow and advective transport (Fig. 1). The proposed theoretical framework can be extended to other configurations that can be represented as a collection of known flow distributions. Ongoing work seeks to extend the framework to more complex media.

PIC

Figure 1: (a) Representation of a simple 2D porous medium considered in this study, showing the disordered arrangement of disks (gray circles), and the magnitude of the fluid velocity from a high fidelity simulation of Stokes flow rescaled by the mean velocity, u∕⟨u⟩. (b) Zoomed-in view of the red box in (a). (c) Zoomed-in view of the blue box in (b). (d) Schematic of the conceptual model of pipes (cyan squares) associated with pore throats. (e) Same field as in (c), in logarithmic scale. Red color indicates above-average velocity; blue color indicates below-average velocity.

As we can see in Fig. 1 the Stokes flow is resolved to very high resolution. Accurate direct numerical simulation of Stokes flow in the pore scale is itself extremely challenging due to the complex pore microstructure, the indefinite elliptic operators, and complex geometries. In two dimensions, boundary integral equations can be used. But in 3D and for geometries that have random structure, boundary integrals become much more challenging. To address this, we developed a novel numerical scheme for solving the Stokes equation with variable coefficients in the unit box. Our scheme is based on a volume integral equation formulation. Compared to finite element methods, our formulation decouples the velocity and pressure and generates velocity fields that are by construction divergence free to high accuracy, and its performance does not depend on the order of the basis used for discretization. In addition, we employ a novel adaptive fast multipole method for volume integrals to obtain a scheme that is algorithmically optimal and supports non-uniform discretizations. To increase per-node performance, we have integrated our code with both NVIDIA and Intel accelerators. In our largest scalability test, we solved a problem with 20 billion unknowns, using a 14th-order approximation for the velocity, on 2048 nodes of the Stampede system at the Texas Advanced Computing Center. We achieved 0.656 petaFLOPS for the overall code (23% efficiency) and one petaFLOPS for the volume integrals (33% efficiency). This work was a finalist for Best Student Paper at SC14 [89]. Illustrative simulations are shown in Fig. 2.

PIC


Figure 2: Here we illustrate capabilities of the 3D porous media flow solver. From left to right: (1) grey color indicates solid phase geometry, white is pore space, velocity streamlines are superposed; (2) same geometry with clipping to better visualize streamlines; (3) octree leaves; (4) spatial partitioning across different nodes.

PIC


Figure 3: Advection-diffusion in a porous medium. Red and orange areas represent solid phase. Streamlines indicate velocity field, which corresponds to stationary Stokes flow through porous medium microstructure (see Fig. 2). Initial condition is linear superposition of three Gaussians indicated by light blue, light green, and yellow. Velocity is calculated using volume integral equation solver; advection-diffusion problem is solved using a semi-Lagrangian scheme for advection and volume integral equation for diffusion. Left-most image depicts initial condition; others show snapshots in time.

To study transport phenomena in porous media we also need an advection-diffusion solver (Fig. 3). We have designed a novel numerical method for solving the scalar advection-diffusion equation using adaptive mesh refinement. Our solver has three unique characteristics: (1) it supports arbitrary-order accuracy in space; (2) it allows different discretizations for the velocity and scalar advected quantity; (3) it combines the method of characteristics with our volume integral equation formulation; and (4) it supports shared and distributed memory architectures. In particular, our solver is based on a second-order accurate, unconditionally stable, semi-Lagrangian scheme combined with a spatially-adaptive Chebyshev octree for discretization. We have studied the convergence, single-node performance, strong scaling, and weak scaling of our scheme for several challenging flows that cannot be resolved efficiently without using high-order accurate discretizations. For example, we consider problems for which switching from 4th order to 14th order approximation results in two orders of magnitude speedups for a computation in which we keep the target accuracy in the solution fixed. For our largest run, we solve a problem with one billion unknowns on a tree with maximum depth equal to 10 and using 14th-order elements on 16,384 x86 cores on the Stampede system at TACC. This work will appear at SC16 [10].