Back to research highlights

9. Scalable joint parameter–model reduction for Bayesian inverse problems (MIT, UT Austin)

Research thrusts: Advanced methods for inference; Validation, adaptation, and management of models
Research sub-thrusts: Goal-oriented, multifidelity, and multiscale methods for inference; Goal-driven adaptive model reduction

The solution of inverse problems is central to prediction and decision making in a host of applications, ranging from subsurface contaminant remediation to understanding the Antarctic ice sheet’s impact on sea level rise. Indeed, inverse problems formalize the essential task of fusing physical models with observational data. The Bayesian approach to inversion offers a rigorous foundation for quantifying uncertainties in parameters and in subsequent predictions. Yet two major computational challenges have impeded the application of Bayesian inversion to complex and large-scale systems: the scaling of posterior sampling algorithms to high-dimensional parameter spaces and the computational cost of repeated forward model evaluations.

Our recent collaborative work [38] has demonstrated how incomplete or noisy data, the state variation and parameter dependence of the forward model, and correlations in the prior distribution collectively provide useful structure that can be exploited for dimension reduction—both in the parameter space of the inverse problem and in the state space of the forward model.

PIC


Figure 13: Atmospheric remote sensing inverse problem, using satellite observations from GOMOS (Global Ozone MOnitoring System). Here we apply joint parameter and model reduction to characterize the posterior distribution of multiple atmospheric gas concentration profiles.

To this end, we have developed algorithms that jointly construct low-dimensional subspaces of the parameter space and the state space in order to accelerate the Bayesian solution of the inverse problem. A crucial feature of our approach is that the computational cost of posterior sampling is rendered independent of the dimension of the full model state or the parameters. The scalability of this approach is the result of several new insights: first, that parameter reduction, informed by the structure of the inverse problem, should precede parameter reduction; and second, that model reduction should exploit “locality” in two complementary senses—both posterior concentration and input space dimension reduction.

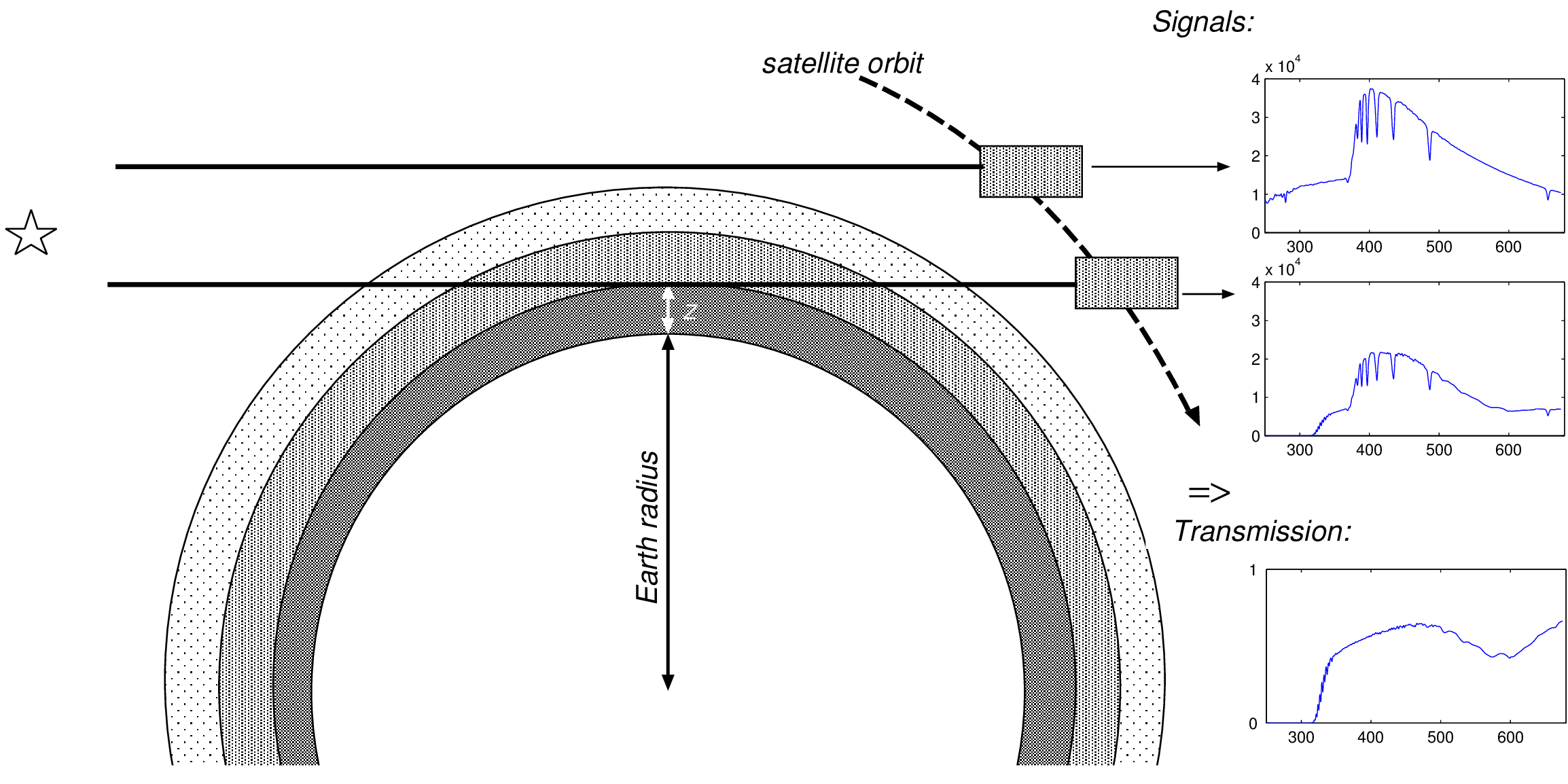
Application to an ice sheet model problem based on the geometry of the Arolla Glacier has demonstrated parameter dimension reduction by multiple orders of magnitude and a hundred-fold reduction in the state dimension. We have also applied the method to atmospheric remote sensing, inferring gas concentration profiles from star occultation measurements (as illustrated in Figure 13). The parameter dimension in this problem is in the thousands and the data number in the tens of thousands, but computational costs scale with an intrinsic dimension of only twenty.

This work—and its application to several complex models—is a result of close collaboration between PI Ghattas (UT-Austin), PIs Marzouk and Willcox (MIT), and former DiaMonD postdocs and now assistant professors N. Petra (UC Merced), T. Cui (Monash), and B. Peherstorfer (Wisconsin). This work is also founded on mathematical results and algorithmic approaches produced by several previous years of DiaMonD support: optimal dimension reduction for linear [128] and linearized [18, 62] inverse problems, online and data-driven model reduction [37], reduced-dimensional Markov chain Monte Carlo sampling [36, 114], and dimension-independent yet geometrically-informed (DILI) sampling schemes [35]. The latter also involves collaboration with DOE laboratory staff at ORNL.